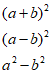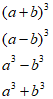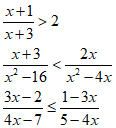Matematyka w klasa pierwszych

Menu główne:

PSO-PP

Przedmiotowy System Oceniania z matematyki obowiazujacy w Zespole Szkół nr 1 w Goleniowie w klasach 1LB, 1TLA, 1TLB, 1THE.

Przedmiotowy System Oceniania
- Matematyka - klasy 1LB, 1TLA, 1TLB, 1THE w roku szkolnym 2017/2018

Kontrakt z uczniami:

1. Ocenie podlegają następujące formy aktywności ucznia: pisemne prace klasowe, sprawdziany, kartkówki, zadania domowe, aktywność na lekcji, projekty edukacyjne.
2. Prace klasowe, sprawdziany, kartkówki i odpowiedzi ustne są obowiązkowe.
3. Praca klasowa jest zapowiedziana, co najmniej tydzień wcześniej i omówiony jest jej zakres - kryteria sukcesu są umieszczane na stronie www.matematyka34.za.pl/m1 .
4. Jeżeli uczeń opuścił pracę klasową z przyczyn losowych, to powinien napisać ją w ciągu tygodnia od dnia powrotu do szkoły (termin uzgadnia z uczniem nauczyciel).
5. Uczeń może poprawić ocenę niesatysfakcjonującą go z pracy klasowej, sprawdzianu lub kartkówki. Poprawy prac odbywają się podczas zajęć dodatkowych (termin podaje nauczyciel - wtorek 15.10).
6. Przy poprawianiu prac klasowych z dwóch ocen wpisanych do dziennika pod uwagę brana jest lepsza z nich.
7. Uczniowie nieobecni na kartkówkach piszą jena następnej lekcji lub w możliwie najbliższym terminie.
8. Nie ma możliwości poprawiania ocen na tydzień przed klasyfikacją semestralną lub roczną.
9. Nie ocenia się uczniów do trzech dni po dłuższej usprawiedliwionej nieobecności.
10. Uczeń ma obowiązek opanowania materiału przerabianego podczas jego nieobecności i samodzielnego uzupełnienia zadawanych zadań domowych.
11. Uczeń ma prawo do dwukrotnego w ciągu półrocza zgłoszenia nieprzygotowania do lekcji. Przez nieprzygotowanie do lekcji rozumiemy: brak zeszytu, brak pracy domowej, brak pomocy do lekcji.
12. Po wykorzystaniu limitu określonego powyżej uczeń otrzymuje: za brak pracy domowej ocenę niedostateczną.
13. Jeśli uczeń nie wykorzystał w I półroczu przysługującego mu limitu nieprzygotowań może go wykorzystać w II półroczu. Jeśli uczeń ani razu w półroczu nie miał stwierdzonego braku zadania otrzymuje pod koniec półrocza ocenę cząstkową bardzo dobrą.
14. Uczeń przez cały rok szkolny, na każdej lekcji matematyki ma obowiązek posiadania przyborów do geometrii: ekierka i linijka, cyrkiel, kątomierz, ołówek, trzy kolorowe kredki, kalkulator.
15. Na lekcji uczeń ma może korzystać ze smartfona lub tabletu z dostępem do Internetu tylko w wyznaczonym przez nauczyciela czasie.
16.Powyższy kontrakt może ulec zmianie na wniosek uczniów i rodziców, uczniów i wychowawcy klasy, dyrektora szkoły lub podczas zmiany zapisów w Wewnątrzszkolnym Systemie Oceniania .

Sposoby i częstotliwość sprawdzania osiągnięć edukacyjnych uczniów.
Sprawdzenie osiągnięć odbywa się poprzez ocenę następujących form aktywności uczniów:

prace klasowe, testy - I semestr - dwie prace klasowe; II semestr - trzy prace klasowe - waga oceny 3
sprawdziany (25 minut) trzy w ciągu semestru - waga oceny 2
kartkówki (do 15 minut), trzy w ciągu semestru - waga oceny 1
odpowiedzi ustne, bez limitu - waga oceny 1
aktywność na lekcji, praca w grupach, bez limitu - waga oceny 1
zadania domowe, bez limitu - waga oceny 1
prace długoterminowe, projekty edukacyjne, przygotowanie się do lekcji odwróconej, bez limitu - waga oceny 2
inne formy aktywności, np. udział w konkursach matematycznych, wykonywanie pomocy dydaktycznych, bez limitu - waga oceny 1

Zależność oceny semestralnej i końcowo rocznej od średniej ważonej

nazwa oceny - ocena - średnia ważona
celujący 6 (od 5,51 do 6,00)
bardzo dobry 5 (od 4,51 do 5,50)
dobry 4 (od 3,51 do 4,50)
dostateczny 3 (od 2 ,51 do 3,50)
dopuszczający 2 (od 1,80 do 2,50)
niedostateczny 1 (od 1 do 1,79)

Na miesiąc przed zakończeniem semestru lub roku szkolnego uczeń zostaje poinformowany o zagrożeniu oceną niedostateczną, jeżeli jego średnia ważona jest mniejsza niż 2,0. Ocena końcowo roczna jest średnią ważoną ocen za II semestr.

Algorytm obliczania średniej ważonej

Obszary aktywności.
Na lekcjach matematyki oceniane będą następujące obszary aktywności uczniów:
1. Kształtowanie pojęć matematycznych - sprawdzanie stopnia zrozumienia pojęć matematycznych.
2. Znajomość i stosowanie poznanych twierdzeń.
3. Prowadzenie rozumowań- sposób prowadzenia rozumowań.
4. Kształtowanie języka matematycznego- ocenianie języka matematycznego na odpowiednim poziomie ścisłości.
5. Rozwiązywanie zadań matematycznych- stosowanie odpowiednich metod, sposobów wykonania i otrzymanych rezultatów.
6. Analizowanie tekstów w stylu matematycznym
7. Rozwiązywanie problemów.
8. Stosowanie wiedzy przedmiotowej w sytuacjach praktycznych.
9. Prezentowanie wyników swojej pracy w różnych formach.
10. Inne formy aktywności np. udział w konkursach przedmiotowych.
11. Przygotowanie do lekcji, aktywność na lekcji, praca w grupach i własny wkład pracy ucznia.

Kryteria oceny prac klasowych, sprawdzianów i kartkówek.
W pracach kontrolnych występują zadania testowej jednej odpowiedzi lub wielokrotnej odpowiedzi oraz zadania otwarte w których oceniane są trzy elementy rozwiązania:
Metoda (wybór prawidłowej drogi postępowania, analiza, wybór wzoru)
Wykonanie (podstawienie do wzoru, obliczenia, również cząstkowe)
Rezultat (wynik, sprawdzenie z warunkami zadania).
Zadanie jest oceniane, gdy obrana jest prawidłowa metoda.
Zadania są punktowane od min. 1 do max. 4 punktów.
Uczeń otrzymuje ocenę zgodnie z punktacją w przeliczeniu na procenty.

*Nauczyciel ma prawo przerwać pisanie pracy kontrolnej uczniowi, jeżeli stwierdzi na podstawie zachowania ucznia niesamodzielność pracy lub zakłócanie przebiegu sprawdzianu (np. sygnałem telefonu komórkowego, rozmowami, odwracaniem się, zaglądaniem do pracy innego ucznia). Stwierdzenie niesamodzielnej pracy lub zakłócanie przebiegu sprawdzianu może być podstawą do wystawienia oceny niedostatecznej.

Uczeń z pisemnych prac klasowych otrzyma informację zwrotną w formie ustnej lub pisemnej z której dowie się:

o dobrych elementach pracy pisemnej,
co wymaga poprawy, nad czym musi jeszcze popracować,
otrzyma wskazówki, jak należy to poprawić,
oraz w jakim kierunku powinien pracować dalej.

Informacja zwrotna będzie ściśle powiązana kryteriami sukcesu.

Uczniowie o obniżonych wymaganiach piszą prace klasowe o obniżonym stopniu trudności (tylko poziom konieczny i podstawowy). Uczniów, którzy mają w orzeczeniu z poradni pedagogicznopsychologicznej wydłużony czas pisania (zaznaczenie w dzienniku lekcyjnym) podczas prac klasowych obowiązuje mniejsza ilość zadań (1-2 zadań). Zadania, które mogą pominąć wskazuje przed każdą pracą klasową nauczyciel. Natomiast podczas kartkówek i sprawdzianów czas zostaje wydłużony o 5min.

Wymagania szczegółówe na poszczególne oceny z matematyki:

Treści nauczania – wymagania szczegółowe


ZAKRES PODSTAWOWY na zielono zaznaczono treści realizowane w klasie pierwszej	ZAKRES ROZSZERZONY na fioletowo zaznaczono treści realizowane w klasie pierwszej
1. Liczby rzeczywiste. Uczeń:
1) przedstawia liczby rzeczywiste w różnych postaciach (np. ułamka zwykłego, ułamka dziesiętnego okresowego, z użyciem symboli pierwiastków, potęg); 2) oblicza wartości wyrażeń arytmetycznych (wymiernych); 3) posługuje się w obliczeniach pierwiastkami dowolnego stopnia i stosuje prawa działań na pierwiastkach; 4) oblicza potęgi o wykładnikach wymiernych i stosuje prawa działań na potęgach o wykładnikach wymiernych; 5) wykorzystuje podstawowe własności potęg (również w zagadnieniach związanych z innymi dziedzinami wiedzy, np. fizyką, chemią, informatyką); 6) wykorzystuje definicję logarytmu i stosuje w obliczeniach wzory na logarytm iloczynu, logarytm ilorazu i logarytm potęgi o wykładniku naturalnym; 7) oblicza błąd bezwzględny i błąd względny przybliżenia; 8) posługuje się pojęciem przedziału liczbowego, zaznacza przedziały na osi liczbowej; 9) wykonuje obliczenia procentowe, oblicza podatki, zysk z lokat (również złożonych na procent składany i na okres krótszy niż rok).	spełnia wymagania określone dla zakresu podstawowego, a ponadto: 1) wykorzystuje pojęcie wartości bezwzględnej i jej interpretację geome tryczną, zaznacza na osi liczbowej zbiory opisane za pomocą równań i nie równości typu: \|x – a\| = b, \|x – a\| < b, \|x – a\| > b, 2) stosuje w obliczeniach wzór na logarytm potęgi oraz wzór na zamianę podstawy logarytmu.
2. Wyrażenia algebraiczne. Uczeń:
1) używa wzorów skróconego mnożenia	spełnia wymagania określone dla zakresu podstawowego, a ponadto: 1) używa wzorów skróconego mnożenia na 2) dzieli wielomiany przez dwumian ax + b; 3) rozkłada wielomian na czynniki, stosując wzory skróconego mnożenia lub wyłączając wspólny czynnik przed nawias; 4) dodaje, odejmuje i mnoży wielomiany; 5) wyznacza dziedzinę prostego wyrażenia wymiernego z jedną zmienną, w którym w mianowniku występują tylko wyrażenia dające się łatwo sprowadzić do iloczynu wielomianów liniowych i kwadratowych; 6) dodaje, odejmuje, mnoży i dzieli wyrażenia wymierne; rozszerza i (w łatwych przykładach) skraca wyrażenia wymierne.
3. Równania i nierówności. Uczeń:
1) sprawdza, czy dana liczba rzeczywista jest rozwiązaniem równania lub nierówności; 2) wykorzystuje interpretację geometryczną układu równań pierwszego stopnia z dwiema niewiadomymi; 3) rozwiązuje nierówności pierwszego stopnia z jedną niewiadomą; 4) rozwiązuje równania kwadratowe z jedną niewiadomą; 5) rozwiązuje nierówności kwadratowe z jedną niewiadomą; 6) korzysta z definicji pierwiastka do rozwiązywania równań typu ; 7) korzysta z własności iloczynu przy rozwiązywaniu równań typu x(x+1)(x-1)=0 ; 8) rozwiązuje proste równania wymierne, prowadzące do równań liniowych lub kwadratowych, np. ;	spełnia wymagania określone dla zakresu podstawowego, a ponadto: 1) stosuje wzory Vi?te'a; 2) rozwiązuje równania i nierówności liniowe i kwadratowe z parametrem; 3) rozwiązuje układy równań, prowadzące do równań kwadratowych; 4) stosuje twierdzenie o reszcie z dzielenia wielomianu przez dwumian x - a; 5) stosuje twierdzenie o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych; 6) rozwiązuje równania wielomianowe dające się łatwo sprowadzić do równań kwadratowych; 7) rozwiązuje łatwe nierówności wielomianowe; 8) rozwiązuje proste nierówności wymierne typu: 9) rozwiązuje równania i nierówności z wartością bezwzględną, o poziomie trudności nie wyższym, niż: \|\|x + 1\|- 2\|= 3, \|x + 3\|+\|x - 5\|>12.
4. Funkcje. Uczeń:
1) określa funkcje za pomocą wzoru, tabeli, wykresu, opisu słownego; 2) oblicza ze wzoru wartość funkcji dla danego argumentu; 3) posługuje się poznanymi metodami rozwiązywania równań do obliczenia, dla jakiego argumentu funkcja przyjmuje daną wartość; 4) odczytuje z wykresu własności funkcji (dziedzinę, zbiór wartości, miejsca zerowe, maksymalne przedziały, w których funkcja maleje, rośnie, ma stały znak; punkty, w których funkcja przyjmuje w podanym przedziale wartość największą lub najmniejszą); 5) na podstawie wykresu funkcji y = f(x) szkicuje wykresy funkcji: y = f(x + a), y = f(x) + a, y = -f(x), y = f(-x); 6) na podstawie wykresu funkcji y = f(x) szkicuje wykresy funkcji: y = f(x + a), y = f(x) + a, y = -f(x), y = f(-x); 7) rysuje wykres funkcji liniowej, korzystając z jej wzoru; 8) wyznacza wzór funkcji liniowej na podstawie informacji o funkcji lub o jej wykresie; 9) interpretuje współczynniki występujące we wzorze funkcji liniowej; 10) szkicuje wykres funkcji kwadratowej, korzystając z jej wzoru; 11) wyznacza wzór funkcji kwadratowej na podstawie pewnych informacji o tej funkcji lub o jej wykresie; 12) interpretuje współczynniki występujące we wzorze funkcji kwadratowej w postaci kanonicznej, w postaci ogólnej i w postaci iloczynowej (o ile istnieje); 13) wyznacza wartość najmniejszą i wartość największą funkcji kwadratowej w przedziale domkniętym; 14) wykorzystuje własności funkcji liniowej i kwadratowej do interpretacji zagadnień geometrycznych, fizycznych itp. (także osadzonych w kontekście praktycznym); 15) szkicuje wykres funkcji f(x) = a/x dla danego a, korzysta ze wzoru i wykresu tej funkcji do interpretacji zagadnień związanych z wielkościami odwrotnie proporcjonalnymi; 16) szkicuje wykresy funkcji wykładniczych dla różnych podstaw; 17) posługuje się funkcjami wykładniczymi do opisu zjawisk fizycznych, chemicznych, a także w zagadnieniach osadzonych w kontekście praktycznym.	spełnia wymagania określone dla zakresu podstawowego, a ponadto: 1) na podstawie wykresu funkcji y = f(x) szkicuje wykresy funkcji: y = \|f(x)\|, y = c · f(x), y = f(cx); 2) szkicuje wykresy funkcji logarytmicznych dla różnych podstaw; 3) posługuje się funkcjami logarytmicznymi do opisu zjawisk fizycznych, chemicznych, a także w zagadnieniach osadzonych w kontekście praktycznym; 4) szkicuje wykres funkcji określonej w różnych przedziałach różnymi wzorami; odczytuje własności takiej funkcji z wykresu.
5. Ciągi. Uczeń:
1) wyznacza wyrazy ciągu określonego wzorem ogólnym; 2) bada, czy dany ciąg jest arytmetyczny lub geometryczny; 3) stosuje wzór na n-ty wyraz i na sumę n początkowych wyrazów ciągu arytmetycznego; 4) stosuje wzór na n-ty wyraz i na sumę n początkowych wyrazów ciągu geometrycznego.	spełnia wymagania określone dla zakresu podstawowego, a ponadto: 1) wyznacza wyrazy ciągu określonego wzorem rekurencyjnym; 2) oblicza granice ciągów, korzystając z granic ciągów typu: ; oraz z twierdzeń o działaniach na granicach ciągów; 3) rozpoznaje szeregi geometryczne zbieżne i oblicza ich sumy.
6. Trygonometria. Uczeń:
1) wykorzystuje definicje i wyznacza wartości funkcji sinus, cosinus i tangens kątów o miarach od 0° do 180°; 2) korzysta z przybliżonych wartości funkcji trygonometrycznych (odczytanych z tablic lub obliczonych za pomocą kalkulatora); 3) oblicza miarę kąta ostrego, dla którego funkcja trygonometryczna przyjmuje daną wartość (miarę dokładną albo - korzystając z tablic lub kalkulatora - przybliżoną); 4) stosuje proste zależności między funkcjami trygonometrycznymi: , oraz ; 5) znając wartość jednej z funkcji: sinus lub cosinus, wyznacza wartości pozostałych funkcji tego samego kąta ostrego.	spełnia wymagania określone dla zakresu podstawowego, a ponadto: 1) stosuje miarę łukową, zamienia miarę łukową kąta na stopniową i odwrotnie; 2) wykorzystuje definicje i wyznacza wartości funkcji sinus, cosinus i tangens dowolnego kąta o mierze wyrażonej w stopniach lub radianach (przezsprowa dzenie do przypadku kąta ostrego); 3) wykorzystuje okresowość funkcji trygonometrycznych; 4) posługuje się wykresami funkcji trygonometrycznych (np. gdy rozwiązuje nierówności typu: ; , ); 5) stosuje wzory na sinus i cosinus sumy i różnicy kątów, sumę i różnicę sinusów i cosinusów kątów; 6) rozwiązuje równania i nierówności trygonometryczne typu: ; ; ; .
7. Planimetria. Uczeń:
1) stosuje zależności między kątem środkowym i kątem wpisanym; 2) korzysta z własności stycznej do okręgu i własności okręgów stycznych; 3) rozpoznaje trójkąty podobne i wykorzystuje (także w kontekstach praktycznych) cechy podobieństwa trójkątów; 4) korzysta z własności funkcji trygonometrycznych w łatwych obliczeniach geometrycznych, w tym ze wzoru na pole trójkąta ostrokątnego o danych dwóch bokach i kącie między nimi.	spełnia wymagania określone dla zakresu podstawowego, a ponadto: 1) stosuje twierdzenia charakteryzujące czworokąty wpisane w okrąg i czworokąty opisane na okręgu; 2) stosuje twierdzenie Talesa i twierdzenie odwrotne do twierdzenia Talesa do obliczania długości odcinków i ustalania równoległości prostych; 3) znajduje obrazy niektórych figur geometrycznych w jednokładności (odcinka, trójkąta, czworokąta itp.); 4) rozpoznaje figury podobne i jednokładne; wykorzystuje (także w kontekstach praktycznych) ich własności; 5) znajduje związki miarowe w figurach płaskich z zastosowaniem twierdzenia sinusów i twierdzenia cosinusów.
8. Geometria na płaszczyźnie kartezjańskiej. Uczeń:
1) wyznacza równanie prostej przechodzącej przez dwa dane punkty (w postaci kierunkowej lub ogólnej); 2) bada równoległość i prostopadłość prostych na podstawie ich równań kierunkowych; 3) wyznacza równanie prostej, która jest równoległa lub prostopadła do prostej danej w postaci kierunkowej i przechodzi przez dany punkt; 4) oblicza współrzędne punktu przecięcia dwóch prostych; 5) wyznacza współrzędne środka odcinka; 6) oblicza odległość dwóch punktów; 7) znajduje obrazy niektórych figur geometrycznych (punktu, prostej, odcinka, okręgu, trójkąta itp.) w symetrii osiowej względem osi układu współrzędnych i symetrii środkowej względem początku układu.	spełnia wymagania określone dla zakresu podstawowego, a ponadto: 1) interpretuje graficznie nierówność liniową z dwiema niewiadomymi oraz układy takich nierówności; 2) bada równoległość i prostopadłość prostych na podstawie ich równań ogólnych; 3) wyznacza równanie prostej, która jest równoległa lub prostopadła do prostej danej w postaci ogólnej i przechodzi przez dany punkt; 4) oblicza odległość punktu od prostej; 5) posługuje się równaniem okręgu (x - a)? + (y - b)? = r? oraz opisuje koła za pomocą nierówności; 6) wyznacza punkty wspólne prostej i okręgu; 7) oblicza współrzędne oraz długość wektora; dodaje i odejmuje wektory oraz mnoży je przez liczbę. Interpretuje geometrycznie działania na wektorach; 8) stosuje wektory do opisu przesunięcia wykresu funkcji.
9. Stereometria. Uczeń:

10. Elementy statystyki opisowej. Teoria prawdopodobieństwa i kombinatoryka. Uczeń:

11. Rachunek różniczkowy. Uczeń: